
Equivalently, it is the subtended angle, from that star's perspective, of the semi-major axis of Earth's orbit. The parallax of a star is taken to be half of the angular distance that a star appears to move relative to the celestial sphere as Earth orbits the Sun. The first successful direct measurements of an object at interstellar distances were undertaken by German astronomer Friedrich Wilhelm Bessel in 1838, who used this approach to calculate the distance of 61 Cygni. Then the distance to the star could be calculated using trigonometry. The difference in angle between the two measurements was known to be twice the parallax angle, which is formed by lines from the Sun and Earth to the star at the vertex. The distance between the two positions of the Earth for the measurements was known to be twice the distance between the Earth and the Sun.
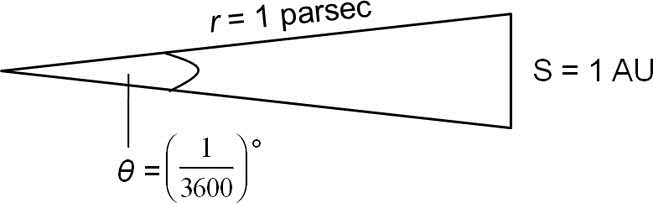
The first measurement was taken from the Earth on one side of the Sun, and the second was taken half a year later when the Earth was on the opposite side of the Sun. One of the oldest methods for astronomers to calculate the distance to a star was to record the difference in angle between two measurements of the position of the star in the sky. Using these two measurements, along with the rules of trigonometry, the length of the adjacent side (the parsec) can be found. The two dimensions on which this triangle is based are the angle (which is defined as 1 arcsecond), and the opposite side (which is defined as 1 astronomical unit, which is the distance from the Earth to the Sun).
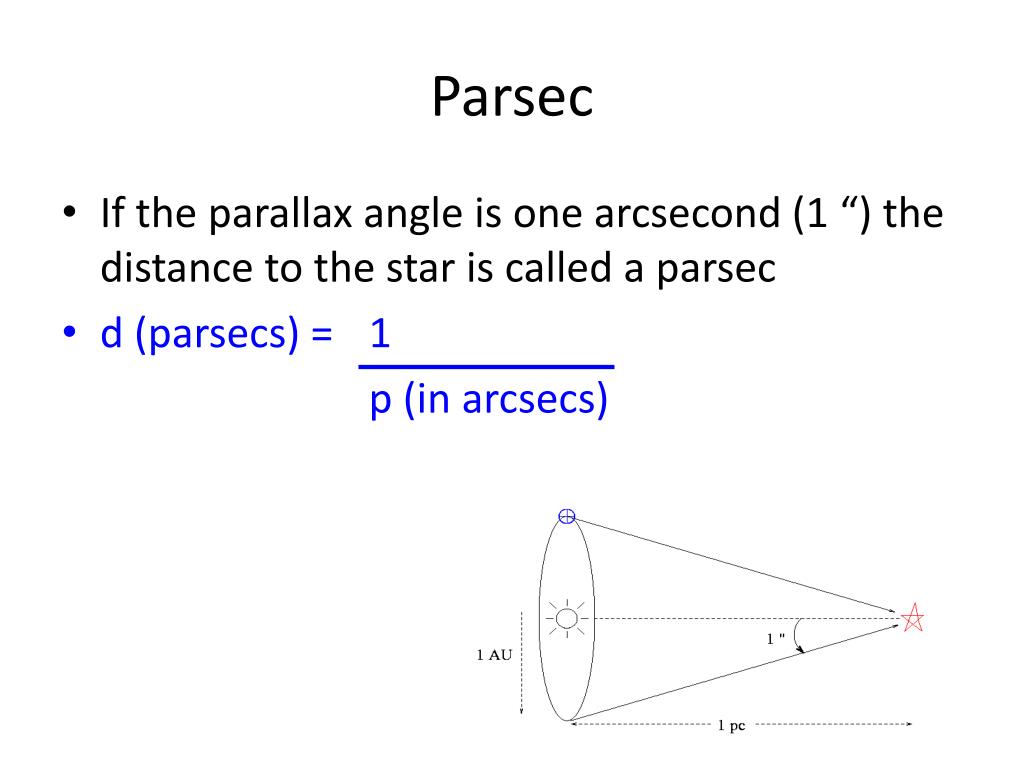
The parsec is equal to the length of the adjacent side of an imaginary right triangle in space.


 0 kommentar(er)
0 kommentar(er)
